You are a special person
Who would have thought that the algorithm we used to verify the files and check the data has now established the blockchain digital currency Empire State Building. The algorithm has many names, such as the general name of the hash algorithm (HASH comes from English). Some of them are also called hash algorithms (images ~~) or hash algorithms (herein we collectively refer to hashes). So now we are going to solve the layers of this algorithm. In this article, we will analyze the characteristics and differences of the four most commonly used cryptographic hash functions in cryptocurrency. But before that, you still need to understand the meaning of the hash.
What is HASH (Hash)
In simple terms, hashing means entering a string of any length to perform a fixed-length output by cryptographic operations. In the case of cryptocurrencies like Bitcoin, the transaction is treated as input and run through a hashing algorithm (bitcoin uses SHA-256) (the algorithm provides a fixed-length output).
First understand how the hash algorithm works. Let's take SHA-256 (256-bit secure hash algorithm) as an example.
In the case of SHA-256, the output always has a fixed 256-bit length no matter how large or small your input is. This is very critical when dealing with large amounts of data and transaction validations. Here we look at the various features of hash functions and how they are implemented in the blockchain.
Cryptographic Hash Algorithm Features
The special features of the hash algorithm make it very suitable for cryptographic applications. The cryptographic hash algorithm has the following features:
Feature 1: Deterministic
This means that no matter how many times you parse a particular input through a hash function, you will get the same result. This is crucial because if you get different hash values ​​each time, it is impossible to track the input.
Feature 2: Fast Calculation
The hash function should be able to quickly return the input hash.
Nature 3: Unidirectionality
Unidirectionality refers to the assumption that A is the input data and H(A) is the output hash result. Suppose it is “infeasible†to give H(A) to push A out. (Note that the term “infeasible†is used. Not "impossible").
Because we already know that determining the original input from its hash value is not "impossible". For example.
Assuming you roll the dice, the output is a hash of the numbers that appear on the dice. How will we determine the original number? Quite simply, all you have to do is find the hash of all numbers from 1-6 and compare them. Since the hash function is deterministic, the input hash is always the same, so we can simply compare the hash and find the original input.
However, this only works if the given amount of data is very small. What happens when you have a lot of data? Suppose you are dealing with a 128-bit hash. The only way to find the original input is to use "violence groups." Violent quarrel basically means that you must pick a random input, hash it, and then compare the output with the target hash and repeat until a match is found.
If you use this violent method:
The best result: You may get the answer on your first attempt, but this is only a theoretical possibility, because his probability is 2 of 1 128th (calculate himself).
The worst case: You get the answer after 2 ^ 128 - 1 times. Basically, this means that you will find your answer at the end of all data.
Average scenario: After 2 ^ 128/2 = 2 ^ 127 times, you will find it somewhere in the middle. From this perspective, 2 ^ 127 = 1.7 * 10 ^ 38. In other words, this is a huge number.
Therefore, although one-way sex can be broken through violent methods, there must also be huge computational effort.
Property 4: Avalanche effect.
Even if you make small changes to the original input data, the results of the hash vary greatly. Let's test it with SHA-256:

Even if you just change the case of the first letter of the input, see how it affects the output hash.
This feature is also known as the avalanche effect.
Nature 5: Collision Avoidance
Given two different inputs A and B, where H(A) and H(B) are their respective hash, it is not feasible that H(A) equals H(B). This means that in most cases, each input will have its own unique hash. Why do we say "mostly"? To understand this, we need to know what is "birthday paradox."
What is the birthday paradox?
If you meet any stranger on the street, then you are very unlikely to have the same birthday. In fact, assuming that all days of the year have the possibility of a birthday, the chance for another person to share your birthday is 1/365, which is 0.27%: the probability is very low.
However, if you gather 20-30 people in one room, the chances of two people sharing the same birthday will increase dramatically.
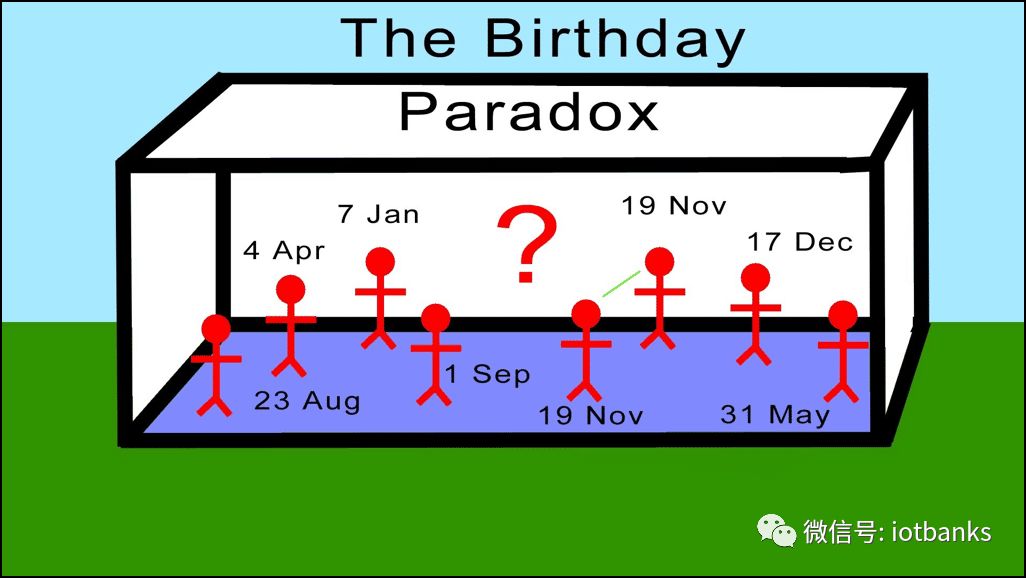
Birthday paradox
This is based on a simple probabilistic principle:
Assuming you have N different possibilities for an event, then you need the square root of N random terms so that they have a 50% collision probability.
Therefore, when applying this theory to your birthday, you have 365 different birthday possibilities, so you only need Sqrt(365), which is about 23%, and the probability of randomly choosing two people to share a birthday is 50%.
Assuming you have a 128-bit hash, there are 2^128 different possibilities. By using the birthday paradox, you have a 50% chance of breaking the anti-collision mechanism in the case of sqrt(2^128) = 2^64.
As you can see, breaking anti-collision is much easier than breaking unidirectionality. So, if you use a function such as SHA-256, suppose that if H(A) = H(B) then A = B is considered to be true.
So how do you create an anti-collision hash function? For this we use a structure called Merkle-Damgard.
What is the Merkle-Damgard structure?
This structure is very simple and follows the following principle: Given the anti-collision hash function of the short message, we can construct an anti-collision hash function for long messages.

Picture source:youtube
With the above chart in mind, note the following:
The larger message M is decomposed into smaller blocks of m[i].
The hash function H consists of many smaller hash functions "h".
"h" is a smaller hash function, also known as a compact function, which receives a small message and returns a hash.
The first hash function "h" (circled in the figure above) receives the first message block (m [0]) and adds a fixed value IV and returns a hash value.
Hash is now added to the second message block and passed through another hash
Function h, and this continues until the last message block, where the pad PB is also added to the message.
The output of each compression function h is called a link variable.
Fill blocks are a series of 1's and 0's. In the SHA-256 algorithm, PB is 64 bits long.
The output of the hash compression function h is the output of the large message M.
Now that you understand the characteristics of the hashing method and the cryptographic hashing function, let's familiarize yourself with some of the most commonly used cryptographic hashing functions in cryptocurrencies.
First list several cryptographic hashing algorithms:
MD 5: It produces a 128-bit hash. After the ~2^21 hash, the anti-collision mechanism is broken.
SHA 1: Generates a 160-bit hash. After 2^61 hashes, the anti-collision mechanism is broken.
SHA 256: Generates a 256-bit hash. This is currently being used by Bitcoin.
Keccak-256: Generated 256-bit hash, currently used by Ethereum.
RIPEMD-160: Generates 160 outputs for use by bitcoin scripts (and SHA-256).
CryptoNight: The hash function used by Monero.
Secure Hash Algorithm (SHA)
The secure hash algorithm is a series of cryptographic hash functions of the United States Federal Information Processing Standard (FIPS) issued by the National Institute of Standards and Technology (NIST). SHA consists of the following algorithms:
SHA-0: Refers to the original 160-bit hash function named "SHA" published in 1993. It was withdrawn shortly after its publication due to an undisclosed "major defect" and replacing it with the later revised version of SHA-1.
SHA-1: Introduced when SHA-0 transmission failed. This is a 160-bit hash function, similar to the earlier MD5 algorithm. This is part of a digital signature algorithm designed by the National Security Agency (NSA). However, people noticed that the weaknesses of encrypted graphics were soon abandoned.
SHA-2: Now let's look at one of the most popular categories in the hash function. It was designed by the NSA using the Merkle-Damgard example. They are two family of hash functions with different word sizes: SHA-256 and SHA-512. Bitcoin uses SHA-256
SHA-3: Previously known as keccak, it was selected in 2012 after open competition from non-NSA designers. It supports the same hash length as SHA-2, and its internal structure is very different from the rest of the SHA series. Ethereum uses this hash function.
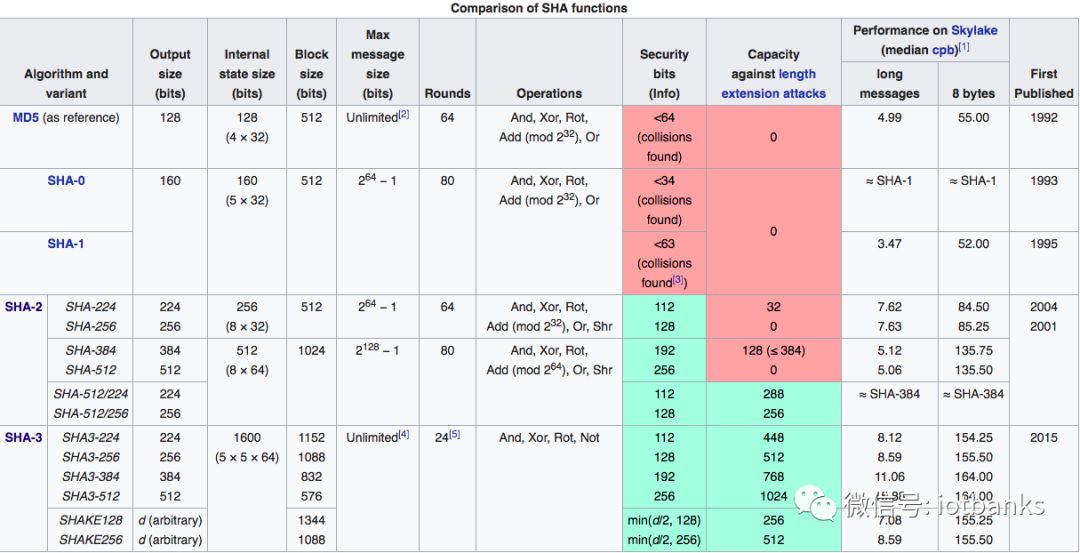
Image source: Wikipedia
Let's take a closer look at SHA-256 and SHA-3.
SHA-256
SHA-256 is a SHA-2 function that uses 32 words instead of SHA-512 with 64-bit words. Bitcoin uses SHA-256 in the following two situations:
mining.
Create an address.
mining:
Bitcoin mining involves miners solving complex computational problems to find a block and then attach it to the Bitcoin blockchain. This is what we often call proof-of-work, which involves the calculation of the SHA-256 hash function.
Create bitcoin address;
The SHA-256 hash function is used to hash Bitcoin public keys to generate public addresses. Hash keys add an extra layer of protection for identity authentication. In addition, the length of the hash address is only shorter than the better stored bitcoin public key.
SHA-256 running example:
Input: Hi
Output: 98EA6E4F216F2FB4B69FFF9B3A44842C38686CA685F3F55DC48C5D3FB1107BE4
SHA-3
As mentioned above, this algorithm was formerly known as keccak and was used by Ethereum. It was created after a non-NSA designer's open competition. SHA-3 uses a "sponge mechanism."
What is a sponge mechanism?

Image source: Wikipedia
The sponge function is a type of algorithm with a limited internal state that takes an input stream of arbitrary length and produces an output stream of a predetermined length.
Before we continue, we need to define some terms:
We know that in the sponge function, the data is "absorbed" into the sponge and the result is "extruded."
So there is an "absorption" phase and a "squeeze" phase.
SHA-3 Example:
Input: Hi
Output: 154013cb8140c753f0ac358da6110fe237481b26c75c3ddc1b59eaf9dd7b46a0a3aeb2cef164b3c82d65b38a4e26ea9930b7b2cb3c01da4ba331c95e62ccb9c3
RIPEMD-160 hash function
RIPEMD is a series of cryptographic hash functions developed by Hans Dobbertin, Antoon Bosselaers and Bart Preneel of Leuven, Belgium, at the COSIC research group at Katholieke University in Leuven, and was first published in 1996.
Although RIPEMD is based on the design principles of MD4, its performance is very similar to SHA-1. RIPEMD-160 is a 160-bit version of this hash function and is commonly used to generate bitcoin addresses.
The Bitcoin public key first runs through the SHA-256 hash function and then runs through the RIPEMD-160. The reason for this is because the 160-bit output is much smaller than 256-bit, which helps save space.
In addition, RIPEMD-160 is a unique hash function that produces the shortest hash and its uniqueness is still fully guaranteed.
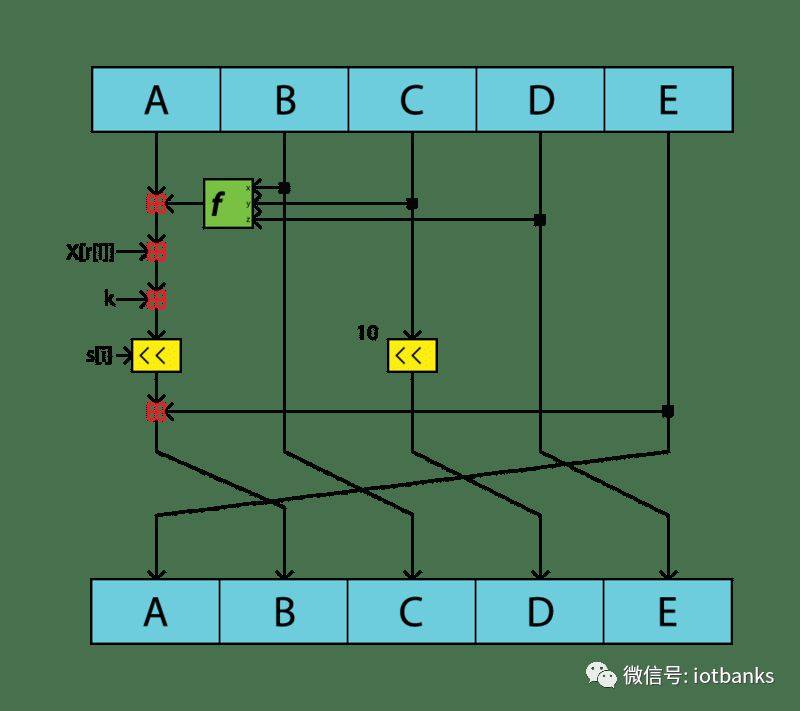
Image source: Wikipedia
The above image shows a sub-block snapshot of the RIPEMD-160 hash algorithm compression function.
RIPEMD-160 example:
Input: Hi
Output: 242485ab6bfd3502bcb3442ea2e211687b8e4d89
CryptoNight hash function
Now we have the CryptoNight hash function used by Monero. Unlike bitcoin, Monero wants their mining to be as unfavorable to the GPU as possible. The only way they can do this is to make their hashing algorithm hard to remember.
Enter CryptoNight
CryptoNight is a memory hardware hash function. It is designed to be computationally inefficient on GPU, FPGA and ASIC architectures. CryptoNight works as follows:
The algorithm first initializes a large register with pseudo-random data.
Afterwards, a large number of read/write operations occur at pseudo-random addresses
Included in the scratch pad.
Finally, the entire register is hashed to produce the final value.
The following figure shows a schematic of the CryptoNight hashing algorithm.
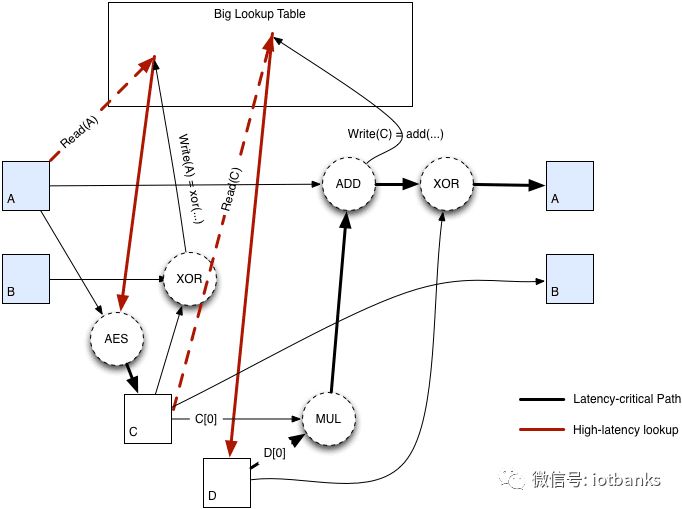
A schematic of the CryptoNight hashing algorithm.
Image credit: Dave's Data
CryptoNight instance:
Enter: This is a test
Output: a084f01d1437a09c6985401b60d43554ae105802c5f5d8a9b3253649c0be6605
in conclusion
The four most commonly used hashing algorithms in cryptocurrency are basically here. Having a basic understanding of the way they work will allow us to better understand the differences between various digital currencies (such as mining).
Closed Pod Electric Vape 3.5ml Pod
Closed Pod Electric Vape 3.5Ml Pod,2 In 1 Vape,Smoking Succedaneum E-Cigarette,Vaporizer E-Cigarette
KENNEDE ELECTRONICS MFG CO.,LTD. , https://www.axavape.com