Google engineers machine learning dry goods: from the three aspects of expressiveness, trainability and generalization

This article is a blog post by Google brain engineer Eric Jiang. Combining current monitoring, unsupervised, and intensive learning progress, he talks about his framework for measuring machine learning research: 1 Expressivity, 2 Trainability, and/or 3 Generalization. This article may be one of the best machine learning techniques and research summaries of the year, worth learning and reference.

When I read a machine learning paper, I would ask myself whether the contribution of this paper belongs to: 1) Expressivity, 2) Trainability, and/or 3) Generalization. I learned this classification from Google Brain colleague Jascha Sohl-Dickstein and introduced the term in this article. I found that this classification effectively considers how individual research papers (especially in theory) relate the sub-areas of AI research (eg, robotics, generative models, NLP) to a large picture.

In this blog post, I will discuss how these concepts can be combined with current (as of November 2017) supervised learning, unsupervised learning, and machine learning research for intensive learning. I think that generalization consists of two categories: "weak generalization" and "strong generalization", which I will discuss separately. This table summarizes my views on things: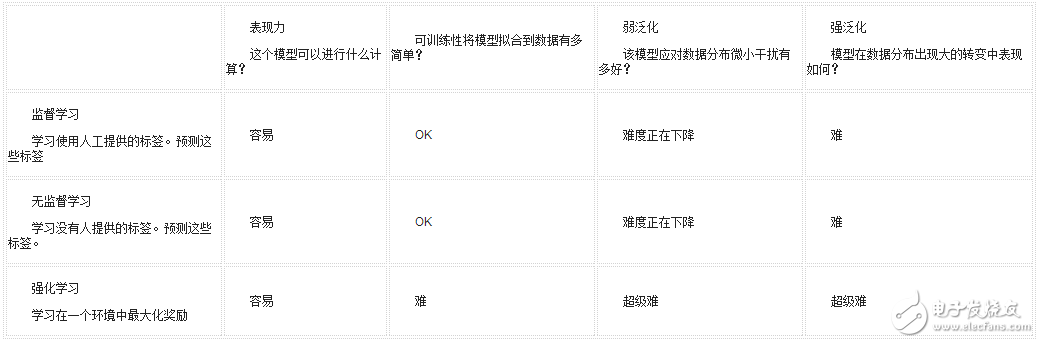



I am very grateful to Jascha Sohl-Dickstein and Ben Poole for their feedback and editing for this article, and to Marcin Moczulski for his helpful discussion on the trainability of RNN.

This article covers a wide range of research and is largely judged by my personal opinion. Therefore, it is important to emphasize that any factual errors in the text are my own and do not reflect the opinions of my colleagues and proofreaders. If you have questions and suggestions that you would like to discuss, please feel free to provide feedback or send an email in the comments - I am writing this article for learning.

Expressiveness: What calculations can this model perform?

Expressivity embodies the complexity of a function that can be computed by a parametric function such as a neural network. Deep neural networks increase exponentially with increasing depth, which means that most of the supervised, unsupervised, and reinforcement learning problems that everyone is studying today can be fully expressed with medium-scale neural networks [2]. One of the evidences is that deep neural networks can memorize very large data sets.

Neural networks can represent a wide variety of things: continuous, complex, discrete, and even random variables. With the study of generation modeling and Bayesian deep learning over the past few years, deep neural networks have been used to construct probabilistic neural networks and have produced incredible generation modeling results.

The latest breakthrough in generation modeling demonstrates the powerful expressiveness of neural networks: neural networks can output extremely complex data manifolds (audio, images) that are almost indistinguishable from real data. The following is the output of the recent GAN architecture proposed by NVIDIA researchers:

This result is not perfect (note the distorted background), but not far from the final goal. Similarly, in the audio synthesis task, the audio samples generated by the latest WaveNet model sound the same as real people.

Unsupervised learning is not limited to generative modeling. Some researchers, such as Yann LeCun, renamed unsupervised learning "predictive learning," which can infer past, estimate present or predict future. However, since many unsupervised learning focuses on predicting extremely complex joint distributions (past or future images, audio), I believe that generation modeling is a fairly good benchmark for measuring unsupervised field performance.

The neural network seems to be sufficient to express reinforcement learning. A small network (2 convolutional layers and 2 fully connected layers) is powerful enough to solve Atari and Mujoco control tasks (although there are many shortcomings in its training, we will talk about this later).

Looking at it alone, expressivity is not an interesting issue in itself. We can increase performance by adding more layers, more connectivity, and other methods to the network. The challenge we face now is to make the neural network show enough training and test data sets under the premise that the control training is not too difficult. For example, even if a deep fully connected network has enough power to remember the training set, it seems that a two-dimensional convolution is needed to make the image classification model generalizable.

Expressiveness is the easiest problem to deal with (adding more layers!), but it is also the most mysterious: we don't have a good way to measure how much (and what kind of expressiveness) a given task requires. What kind of problem requires a neural network that is orders of magnitude larger than the neural network we use today? Why do these problems require such a large amount of calculations? Does the current neural network have enough expressive power to achieve intelligence similar to humans? Does solving a generalization problem require a super-powerful model?

The number of neurons in the brain (1e11) is many orders of magnitude larger than that of a large neural network (Inception-ResNet-V2 has about 25e6 ReLU units). Moreover, the ReLU unit simply cannot match the complexity of human neurons. A single biological neuron with its dendrites, axons and various neurotransmitters has incredible expressive power. The mites implement a collision detection system in a single neuron that flies better than any of the drone systems we build. Where does this expression come from? To achieve human intelligence, how strong is the neural network?

Trainability: Given a fully expressed model space, can we find a good model?

A machine learning model is any computer program that learns functions from data. During the “learning” period, we look for a better model that can make use of the knowledge in the data to make decisions from a potentially huge model space. This search process is usually defined as solving the optimization problem of the model space.

Several types of optimization

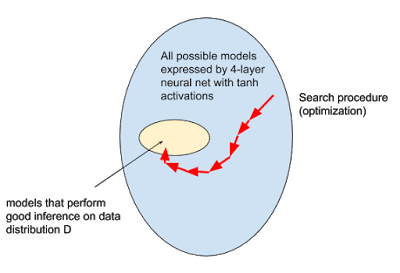
A common approach, especially in deep learning, is to define some scalar metrics to evaluate the "advantages" of the model. These "advantages" are then maximized (or "minimized bad") using numerical optimization techniques.

A specific example: Minimizing the average cross entropy error is a standard method for training neural network classification images. The purpose of this is that when the model x dataset has the lowest cross entropy loss, it does what we really want, such as correctly classifying the image with a certain degree of precision and recalling it on the test image. In general, evaluation metrics cannot be directly optimized (the most obvious reason is that we cannot access the test data set), and alternative functions like cross entropy on the training set can.

Finding a good model (ie training) is ultimately equated with optimization – that's the truth! But... the goal of optimization is sometimes difficult to determine. In supervised learning, a typical scenario is down-sampling, in which case it is difficult to define a scalar quantity that allows humans to perceive "perceptual loss" from a particular downsampling algorithm. It is exactly the same. Similarly, super-resolution and image synthesis are difficult, because it is difficult to maximize "advantage/good". Imagine writing a function that determines the extent to which an image is "photoreal"! In fact, the debate has been intensifying on how to measure the quality of the generated models (for images, audio).

In recent years, the most popular technique for solving this problem is a co-adaptation approach, which converts the optimization problem into a solution point between two non-stationary distributions, and these non-stationary distributions are Co-evolution (in tandem) [3]. Use an intuitive metaphor to explain why this is “natural” and think about the ecological evolution between predator species and the species being hunted. At first, predators became smarter, so they can effectively capture prey. Then, the prey becomes smarter and escapes the hunter. In this way, the species evolved in concert, and the end result is that both species become smarter.

The generated confrontation network also works on a similar principle, by which the clear definition of perceptual loss objectives is avoided. Similarly, competitive self-play in reinforcement learning uses this principle to learn a large number of rich behavioral actions. Although the optimization goal has now been implicitly specified, it is still an optimization issue, and machine learning practitioners can reuse familiar tools such as deep neural networks and SGD.

Evolutionary strategies often consider optimization as an optimization-as-a-simulation. The user specifies a dynamic system on a population of models and updates the population according to the rules of the dynamic system at each time step of the simulation. Models may or may not affect each other. As the simulation progresses, it is hoped that the dynamics of the system will eventually induce this overall convergence into a "good model."

To understand the evolutionary strategy (ES) in the context of reinforcement learning, you can refer to David Ha's "A Visual Guide to Evolution Strategies" and the "References and Further Reading" section is great!

Current research and work summary

The “direct” goal of the feedforward network and supervised learning has basically solved the trainability (I have come to this conclusion empirically, not a theoretical summary). Some of the breakthrough work released in 2015 (Batch Norm, ResNets, Good Init) has been widely used in the training of feed-forward networks today. In fact, deep networks with hundreds of layers can now minimize training errors for large-scale classified data sets to zero.

On the other hand, RNN is still very tricky, but the research community is making great progress, putting LSTM into a complex robot strategy and expecting it to "work properly" is no longer a crazy thing. It's incredible to think about it. In 2014, not many people have confidence in the trainability of RNN. In the past decade, there has been a lot of work that shows that RNN is very difficult to train. There is evidence that a large number of different RNN architectures are equally expressive, and any performance difference is due to the fact that some architectures are easier to optimize than others [4].

In unsupervised learning, the output of the model is usually (but not always) larger—for example, 1024 x 1024 pixels, a huge sequence of speech and text. It is therefore unfortunate that unsupervised models are also more difficult to train.

A major breakthrough in 2017 was that GAN is now easier to train. The most common improvement is the simple modification of the original Jensen-Shannon divergence target: absolute deviation with margin, and Wasserstein distance. NVIDIA's recent work extends Wasserstein-based GAN to reduce the sensitivity of the model to various parameters such as BatchNorm parameters and architectural choices. Stability is very important for practical and industrial applications – because of stability, it is believed that this approach will be compatible with future research ideas or applications. In summary, these results are exciting because they show that the generator neural network has enough expressive power to generate the correct images, and preventing their bottlenecks is only a matter of trainability. Trainability may still be a bottleneck – unfortunately, for neural networks, it is difficult to judge whether the model is not performing enough, or we have not trained it.

Due to the high variance Monte Carlo gradient estimator, latent discrete variable inference is also difficult to train in neural networks. However, in recent years, from GAN to language modeling, to memory-enhanced neural networks, to reinforcement learning, various architectures have begun to regain attention. From an expressive point of view, discrete representations are very useful, and we can now train fairly reliably, which is very good.

Unfortunately, deep reinforcement learning is still quite backward in terms of pure trainability, not to mention the ability to generalize. For those environments where the time step is over 1, we are looking for a model that is optimized for reasoning. There is an internal optimization process in which model reasoning leads to optimal control, while an external optimization loop uses only the database that the agent sees to learn the best model.

Recently, I added an extra dimension to the continuous robot control task, which reduced the performance of my reinforcement learning algorithm from >80% to 10%. Intensive learning is not only difficult to train, but also unstable! Because the optimization randomness is too strong, we can't even get the same result with different random seeds, so our strategy is to report the distribution of reward curves in multiple trials, using different random seeds. The same algorithm, because of different deployments, performs differently in different environments, so the RL scores reported in the literature should be viewed with a critical eye.

The problem of trainability in reinforcement learning has still not been solved. We still can't expand the problem a little bit, and then expect the same learning process to do the same thing 10 times.

If we think of RL as a pure optimization problem (and then worry about generalization and complex tasks), the situation is still very tricky. Suppose there is an environment where a sparse reward can only be obtained at the end of episode (for example, looking after a child and getting paid after the parents return home). The number of actions (and the corresponding results of the environment) increases exponentially with the duration of the event, but only a few of these sequences of actions correspond to success.

Therefore, estimating the strategy gradient at any point in the model optimization range requires a large number of samples in the action space before a useful learning signal is obtained. This is like Monte Carlo expectation to calculate the probability distribution, but (on all motion sequences) the quality is concentrated on the delta distribution. When there is no overlap between the proposal distribution and the reward distribution, the finite sample Monte Carlo strategy gradient estimate does not work at all, no matter how many samples are collected.

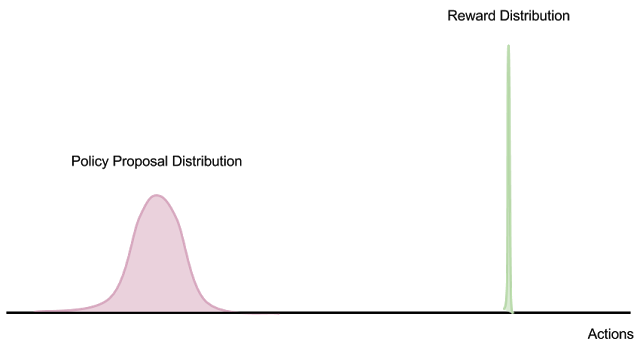
In addition, if the data distribution is non-stationary (as in the case of the off-policy learning algorithm with replay buffer), collecting "bad data" introduces an unstable feedback loop in the external optimization process.

From the perspective of optimization rather than Monte Carlo estimates, the same is true: there is no a priori in the state space (for example, an understanding of the world or a clear indication to the agent), the whole optimization looks like "Switzerland" Cheese" - a convex optima "small hole" is surrounded by a large number of plateaus, where the strategy gradient is useless. This means that there is essentially no information in the entire model space (because the learning signal is very uniform throughout the model space and the non-zero area is very small).

If we don't develop a good representation that we can learn, we might as well use a random seed and a random strategy loop until we find a good model that just falls within these cheese holes. In fact, the intensive learning baseline suggests that our optimization landscape may seem like this.

I believe that from a purely optimized perspective, RL benchmarks like Atari and Mujoco do not really push the limits of machine learning, just to solve a single monolithic policy problem, which can be said to be quite sterile. Optimize performance under the environment. In this case, the selection pressure of the model “generalization” is very small, making the problem a pure optimization problem rather than a real difficult ML problem.

It's not that I like to use generalization to complicate the trainability of reinforcement learning (it's certainly not easy to debug!), but I think learning to understand the environment and understanding tasks is the only way to enhance learning and dealing with real-world robot problems.

Comparing this with supervised learning and unsupervised learning, we can easily obtain learning signals no matter where we are in the model search space. The proposal distribution of the Minibatch gradient overlaps with the gradient distribution non-zero. If we use a small batch size of 1 SGD, the probability of sampling the conversion with a useful learning signal is 1/N, where N is the size of the data set. We can solve problems by simply throwing a lot of calculations and data, making our approach a good solution. In addition, improving the perceptual generalization of the lower layers, by "bootstrapping" on the lower-level features, may actually have the effect of reducing the variance.

In order to solve high-dimensional and complex RL problems, generalization and general perceptual understanding must be considered before dealing with numerical optimization problems. We need to reach the point where each data point provides a non-zero number of bits for the RL algorithm, and when the task is very complex (no more data is collected at the exponential level), the importance sampling gradient can be easily implemented. Only in this way can we reasonably assume that we can successfully solve the problem through violent calculations.

Learning from demonstration, imitation learning, inverse reinforcement learning, and interaction with natural language instructions may provide some means to quickly introduce the starting policy into the acquisition. At some point in the learning signal, or in such a way to shape the search space. For example, the environment provides a reward of 0, but observations produce some information that helps the planning module of the model to derive inductive biases.

All in all, on the issue of trainability: supervised learning has been easy; unsupervised learning is still difficult, but we are working hard; intensive learning is very bad.

Generalization: the core of machine learning itself

Generalization is the most profound of the three issues and the core of machine learning itself. Simply put, generalization is how a model is trained on a training dataset and how it performs on the test dataset.

There are two different scenarios when discussing generalization: 1) training and test data are extracted from the same distribution (we only need to learn this distribution from the training data), or 2) training and test data from different distributions (We need to extend from the training set to the test distribution). These two cases correspond to (1) "weak generalization" and (2) "strong generalization" as I say below. This way of classifying generalization can also be called "interpolation vs. extrapolation" or "robustness vs. understanding".

Weak generalization: In both cases, how good is the model's small perturbation to the data distribution?

In "weak generalization," we usually assume that training and test data samples are extracted from the same distribution. In the real world, however, there are almost always differences between training and test distributions, even within large sample sizes.

These differences can come from sensor noise, changes in ambient light conditions, gradual wear and tear of objects, and changes in lighting conditions. In the other case, differences can be generated by an adversary. Because anti-jamming is almost imperceptible to human vision, we can classify confrontation samples as "extracted from the same distribution."

Therefore, it is useful to use “weak generalization” as a “disturbance” to assess the distribution of training in practice:

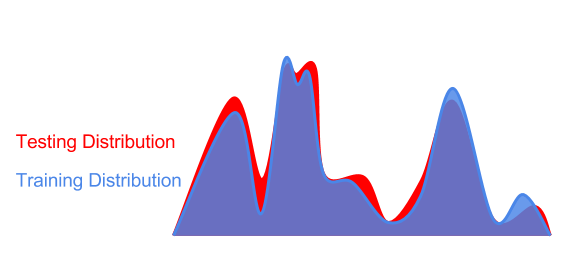
Interference with the test data distribution may also result in optimized interference (the lowest point is the best).

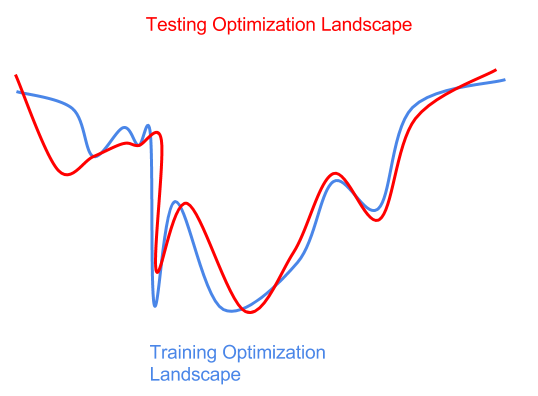
In fact, we don't know in advance that test distribution interference poses some difficulties for optimization. If we are too aggressive in optimizing the training environment (sharp global minimum to the left of the blue curve), then we will get a suboptimal model for the test data (sharp local minimum on the red curve). Here, we have over-fitting the training distribution or training data samples, and there is no test distribution that is generalized to interference.

"Regularization" is the technique we use to prevent overfitting. Since we don't have any prior information about test disturbances, the best thing we can usually do is try to train random disturbances in the training distribution, and hope that these disturbances cover the test distribution. Random gradient descent, dropout, weight noise, activation noise, and data enhancement are all regularization operators commonly used in deep learning. In reinforcement learning, randomizing the simulation parameters makes the training more robust. In his ICLR 2017 speech, Zhang Chiyuan pointed out that formalization is “anything that makes training more difficult” (compared to the traditional view of “restricting model capacity”). Basically, making things harder to optimize can improve generalization performance.

This is really disturbing - our "generalization" approach is quite crude, equivalent to "optimizer lobotomy". What we do is basically to adjust the optimizer, and then hope that its interference with the training process just prevents over-fitting. Moreover, improving the trainability of the model allows you to sacrifice the generalization! Looking at the (weak) generalization problem in this way does indeed complicate the development of trainable research.

However, if a better optimizer is prone to overfitting, how do we explain why some optimizers seem to reduce training and testing errors? The reality is that any combination of optimization methods and optimizers is in 1) finding a better model area and 2) over-fitting to a specific solution to achieve a balance, and we have no good way to Control this balance.

The most challenging test for weak generalization may be a confrontational attack. In a confrontational attack, the disturbance comes from an opponent "adversary", which performs the worst interference to the data points, making your model perform with higher probability. Not good. We still don't have a deep learning method that can deal with adversarial attacks well, but my instinct is that confrontational attacks can eventually be solved [5].

In terms of theoretical work, some researchers are using information theory to explore the neural network in the training process, the model from "memory" data to "compressed" data. This theory is emerging, although there is still academic debate on whether it is effective. It is intuitively convincing from "memory" and "compression", so this aspect deserves our attention.

Strong generalization: Natural Manifold

In the "strong generalization" test, the data used in the test was derived from a completely different distribution from the training data, but the underlying manifest (or generation process) of the data was the same.

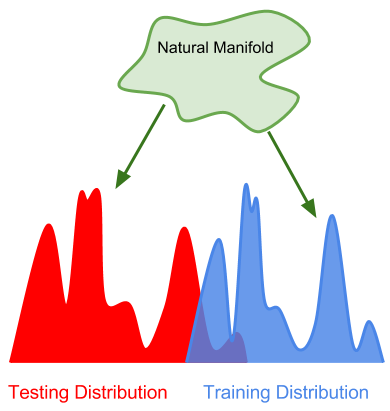
The space of observable data in the world can be described as a very high-dimensional, ever-changing "natural manifold." Although the popularity is huge, it is also highly structured. For example, all the data we observe follows the physical laws of gravitation, objects do not appear in objects, and so on.

Strong generalization can be thought of as to what extent this "super manifold" is captured by a particular model that is trained only on the decimal samples of the data points of the manifold. It should be noted that the image classifier does not need to find Maxwell's equations, it only needs to understand the reality that is consistent with the manifold data.

The modern classification model trained on ImageNet is ok in terms of strong generalization - the model trained on ImageNet does understand the principles of edges, contours and objects, which is why the ImageNet pre-training model is popular. However, there is still a lot of room for improvement in this type of model: the classifiers trained on ImageNet are not universally applicable, the problem of less data learning is still unresolved, and it is still vulnerable to attack against samples. Obviously, our models don't yet understand what they are looking at, but this is the beginning.

Similar to weak generalization, test distributions can be counter-sampled in a manner that counters the greatest difference between training and test distributions. AlphaGo Zero is my favorite example: when testing, it observes data from human players that is completely different from its training distribution (it has never "seen" humans before). Moreover, humans are taking advantage of all their wisdom to take AlphaGo to the undiscovered areas of training data. Although AlphaGo does not explicitly understand what abstract math, rival psychology, or "green" means, it clearly understands how this world is better than human players in a narrow field. If an artificial intelligence system is robust against a skilled human adversary, then I think it has a strong generalization ability.

It is a pity that reinforcement learning research largely ignores the problem of strong generalization. Most benchmarks are static environments with little perceptual richness (for example, humanoid robots don't understand what the world around it or what its own body looks like, except for some joint positions related to reward mechanisms).

I really believe that solving generalization is the key to solving the trainability of reinforcement learning. The more our learning system “knows” the world, the better the ability to acquire learning signals, and perhaps the fewer samples we need. That's why less-shot learning, imitation learning, and learning-to-learn are important: it frees us from violent solutions with large differences and low information.

I believe that to achieve a stronger generalization, two things need to be done:

First, we need to actively derive models of the basic laws of the world from observations and experiments. Symbolic reasoning and causal reasoning seem to be mature research topics, but any kind of unsupervised learning can help. This reminds me of human beings' understanding of the movement of celestial bodies by using the logic inference system (mathematics) to derive the laws of the universe. Interestingly, before the Copernican revolution, humans may initially rely on Bayesian heuristics ("superstitions"), and after we discovered classical mechanics, these "Bayesian" models were abandoned.

Our model-based machine learning approach (trying to "predict" environmental aspects of the model) is still in the "former Copernican era," that is, they are only interpolated based on very shallow statistical superstitions, rather than proposing profound, The general principle is to explain and infer data that may be in the millions of light years or many future time steps. Note that humans do not need a firm grasp of probability theory to derive deterministic celestial mechanics, and this raises the question of whether there is a way to machine learning and causal inference if there is no clear statistical framework.

One way to dramatically reduce complexity is to make our learning system more adaptive. We need to go beyond just optimizing models that predict or act in a static way. We need to optimize models that can be thought, remembered, and learned in real time.

Second, we need to invest enough diversified data on this issue to get the model to develop abstract representations. Only when the environment is rich enough, the correct representation can be developed (although AlphaGo Zero raises the question of how many natural manifolds the agent really needs to experience). Without these limitations, this issue is not clearly defined, and we have the chance to find the right solution by chance.

I don't know that the three-body civilization (see the book "Three-body") has evolved to such a high level of technology, is it because their survival depends on their physical understanding of complex celestial mechanics. Maybe we also need to introduce some celestial movements in our Mujoco&Bullet environment :)

Comment

[1] Some research areas are not suitable for the framework of expressivity, trainability, and generalization capabilities. For example, trying to understand why a model provides an interpretability research for a particular answer. ML clients and policy makers working in high-risk areas (such as medicine, law enforcement) need to understand this, which can also clarify generalization issues: if we find that the diagnostic methods provided by the model and those with human medical professionals will come to these The conclusion is very different, which may mean that the model has an edge case in the derivation process and cannot be generalized. Determining whether the model has learned the right thing is more important than reducing test errors! Differential privacy is another constraint on the ML model. However, in view of the scope of this article, there is not much to say here.

[2] A simple explanation: a fully connected layer of size N, followed by a ReLU nonlinearity, can cut a vector space into N piecewise linear blocks. Add a second ReLU layer, further subdivide the space into N or more blocks, and generate N^2 piecewise linear regions in the input space, and the three layers are N^3. See Raghu et al. 2017 for a detailed analysis.

[3] This is sometimes referred to as a multi-level optimization problem. However, this means an "external" and "internal" optimization loop, and adaptation may occur at the same time. For example, parallel processes on a single machine that communicate asynchronously, or species that are constantly co-evolving in an ecosystem. In these cases, there is no clear "external" and "internal" optimization loop.

[4] seq2seq with attention implements SOTA, but I suspect its strength is trainability, not expressiveness or generalization. Maybe seq2seq without attention can be done just as well in the case of proper initialization.

[5] Here is a way to combat confrontational attacks. Although it does not solve the problem of strong generalization, it is extremely expensive to make calculations against interference. The model and data sections are black boxes. Each time the model is called during reasoning, a model is randomly selected from the trained models and presented to the opponent without telling them which model they got. Models are trained independently of each other and can even adopt different architectures. This makes it difficult to calculate a finite difference gradient because f(x + dx) - f(x) can have any high variance. Furthermore, the gradient between successive gradient calculations will still have a higher variance because different model pairs can be sampled. Another improvement is the use of multimode data (video, multiview, image+sound), which makes it difficult to interfere with the input while maintaining input consistency.